摘要：
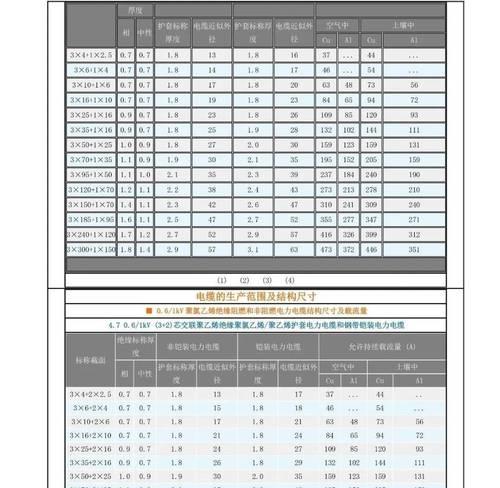
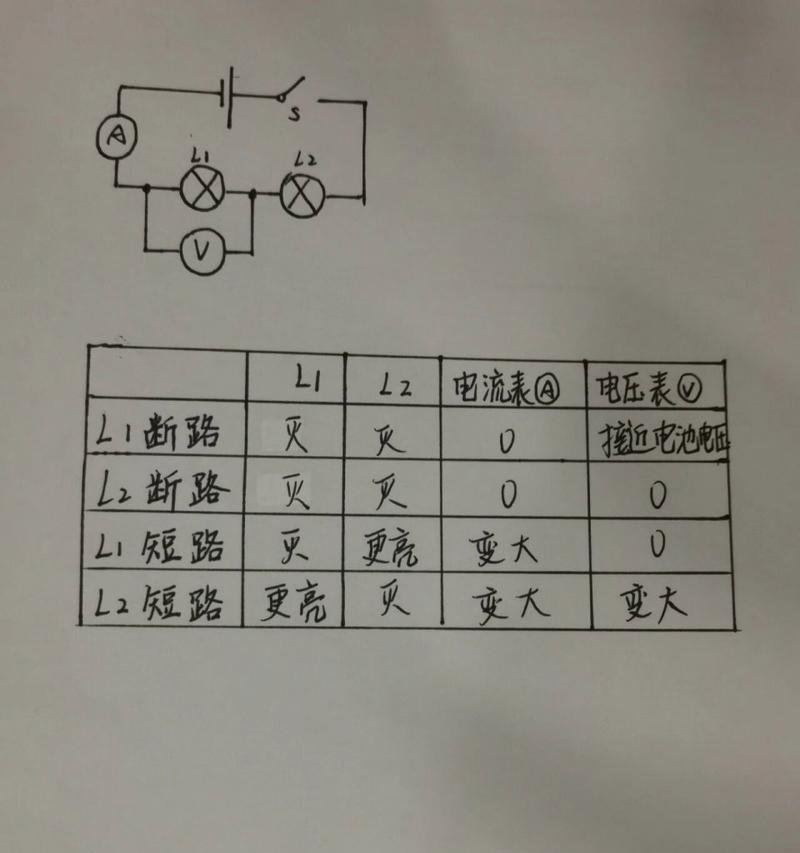
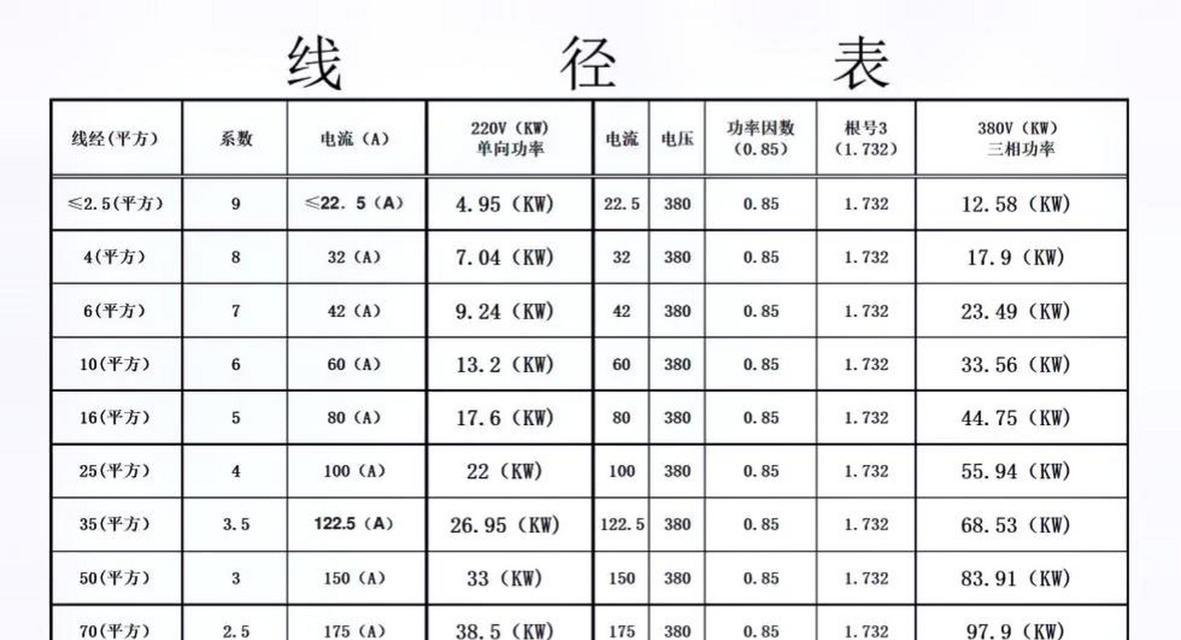
在这个信息量巨大的互联网时代，我们经常需要在数据结构中寻找从一个点到另一个点的最短路径。比如在编程问题中，一个常见的算法问题就是找到从节点A到节点B的最短路径。这里我们以“21号到... 在这个信息量巨大的互联网时代，我们经常需要在数据结构中寻找从一个点到另一个点的最短路径。比如在编程问题中，一个常见的算法问题就是找到从节点A到节点B的最短路径。这里我们以“21号到5.4”的路径为例，探讨如何解决这类问题。
开篇核心突出
在探讨“21号到5.4”的最短路径问题之前，我们要明确本问题并非指实际的地理位置，而是数据结构中的节点连接问题。核心关键词“最短路径”在算法领域代表一种计算图中两点间最短路径长度的算法，而本文将深入解析这一问题。
结构分明、逻辑清晰
一、问题背景介绍
在数据结构和算法的世界里，“最短路径”是一个广泛研究的问题。它被广泛应用于网络路由、地图导航、社交网络分析等多个领域。要解决“21号到5.4”的最短路径问题，首先我们需要理解图论中的基本概念。
二、图论基础
在图论中，“图”是由节点（顶点）和连接节点的边组成的结构。路径是边的序列，从一个节点出发到达另一个节点。若边有方向，则称该图为有向图；若边没有方向，则称为无向图。
三、算法概述
解决最短路径问题的常用算法包括但不限于：迪杰斯特拉（Dijkstra）算法、贝尔曼-福特（Bellman-Ford）算法、弗洛伊德（Floyd-Warshall）算法等。
四、详细步骤解析
1.数据表示
在解决“21号到5.4”的问题前，首先需要将问题转化为图的表示方法。我们可以将节点表示为21号和5.4，并根据问题的具体要求来定义边和它们的权重。
2.选择合适的算法
根据图的大小和特性，选择合适的算法。如果图中不存在负权重的边，那么迪杰斯特拉算法通常是较优选择。
3.实施算法
详细步骤如下：
初始化所有节点的距离为无穷大，除了起点设置为0。
创建一个优先队列，将所有节点加入队列，并按照距离排序。
当队列非空时，重复以下步骤：
从队列中取出距离最小的节点。
更新该节点的邻居节点的距离。
将更新过的节点重新放入优先队列。
4.输出结果
最终，算法会输出从起点到终点的最短路径及其距离。
五、实例分析
为更好地说明问题，我们可以构建一个具体的例子进行分析。假设我们有一个有向图，节点21号与节点5.4之间有多条路径，通过算法我们可以找到哪条是最短的。
六、常见问题解答
Q1:为什么在有负权重边的图中，迪杰斯特拉算法不适用？
Q2:如何在大规模图中高效实现最短路径算法？
七、实用技巧
技巧1：在图中寻找最短路径时，考虑使用哈希表存储节点到起点的最短距离，以提高查找效率。
技巧2：在实现算法时，使用邻接矩阵或邻接表来表示图，根据实际情况选择最合适的数据结构。
八、结语
通过本文的介绍，您应该对如何解决从“21号到5.4”的最短路径问题有了一个全面的认识。无论是理论知识还是实际操作，我们都进行了详细的解析和指导。
在实际应用中，理解并掌握不同的最短路径算法，能够帮助我们更好地解决各种复杂的问题。希望本文能够为您的学习和研究提供帮助，并激发您对算法探索的兴趣。
